In this paper, the combined upshot of Soret and Dufoue of a convective Maxwell nanofluid on a porous perpendicular surface with nonlinear thermal emission was investigated. In the present work, the impact of permeable stretching sheet, nonlinear thermal emission, heat sour sink, Dufour and Soret effect, chemical reaction, Brownian motion and thermophoresis in a convective Maxwell nanofluid flow is widely discussed. The governing equations derived for the problem are highly nonlinear coupled partial differential equations. The governing equations were transformed into ordinary differential equations using Lie symmetry group alterations. The BVP4C MATLAB solver was employed to solve the ordinary differential equations numerically after validating the convergence of the method with existing results in the literature. The numerical results were established and discussed using tables and graphs. It was found that variations in porosity parameter (K), Dufour (Du) and Soret (Sr) improves velocity, temperature and concentration profiles respectively and the present of nonlinear thermal radiation and heat source emit more heat for the flow. Also, it is exciting to report that both porosity (K) and Dufour (Du) parameters has a strong impact on the flow of skin frictions, Nusselt number and Sherwood number. However, the current results may present applications in the areas of petroleum reservoir, heat exchangers, steel industries, cooling applications, nuclear waste disposal and so on.
| Published in | International Journal of Theoretical and Applied Mathematics (Volume 10, Issue 3) |
| DOI | 10.11648/j.ijtam.20241003.12 |
| Page(s) | 38-50 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Soret, Dufour, Heat Source, and Nonlinear Thermal Radiation
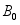 . According to Figure 1, The Maxwell nanofluid is presumed to flow along the x-direction. The Boussinesq approximation is considered, and the flow is fully developed and laminar.
. According to Figure 1, The Maxwell nanofluid is presumed to flow along the x-direction. The Boussinesq approximation is considered, and the flow is fully developed and laminar. 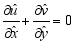 (1)
(1) 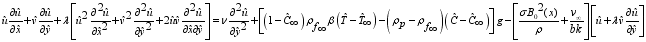 (2)
(2) 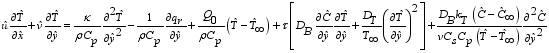 (3)
(3) 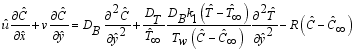 (4)
(4) 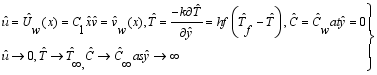 (5)
(5) 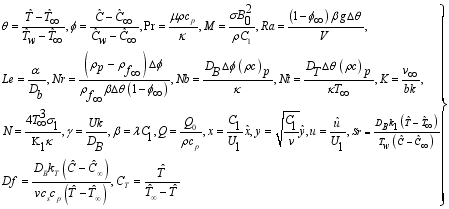 (6)
(6) 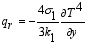 (7)
(7) 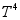 into Taylor’s series expansion In order to linearize equation (7) gives
into Taylor’s series expansion In order to linearize equation (7) gives 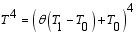 (8)
(8) 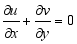 (9)
(9) 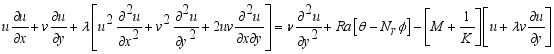 (10)
(10) 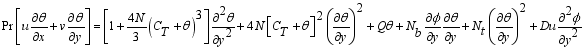 (11)
(11) 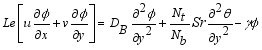 (12)
(12) 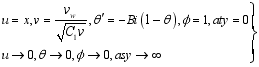 (13)
(13) 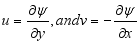 (14)
(14) 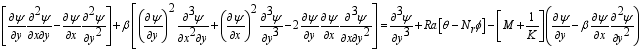 (15)
(15) 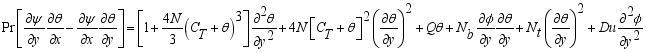 (16)
(16) 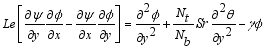 (17)
(17) 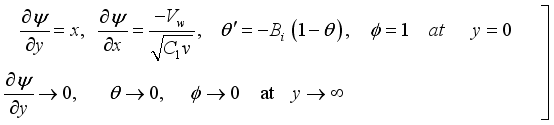 (18)
(18) 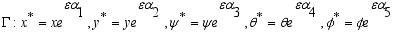 (19)
(19) 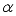 is the real number and
is the real number and 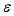 is the parameter of the group we got:
is the parameter of the group we got: 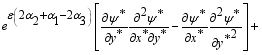
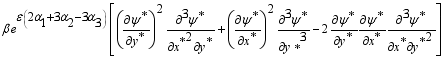
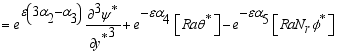
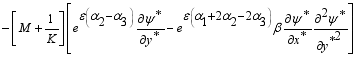 (20)
(20) 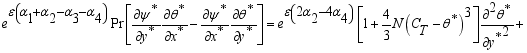
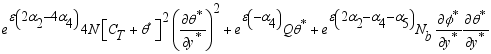
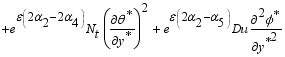 (21)
(21) 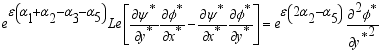
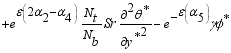 (22)
(22) 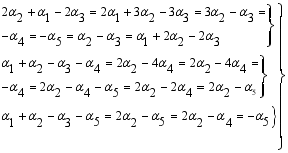 (23)
(23) 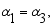
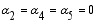 (24)
(24) 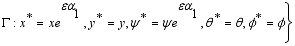 (25)
(25) 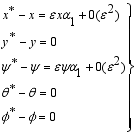 (26)
(26) 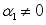 , altering equation (26), the following developed:
, altering equation (26), the following developed: 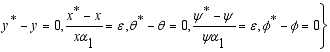 (27)
(27) 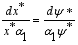 (28)
(28) 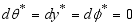 (29)
(29) 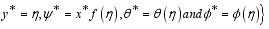 (30)
(30) 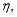 is the similarity variable
is the similarity variable 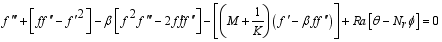 (31)
(31) 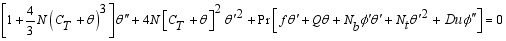 (32)
(32) 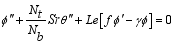 (33)
(33) 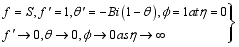 (34)
(34) 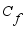 ,
, 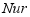 , and
, and 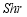 as defined below:
as defined below: 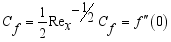 (35)
(35) 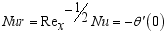 (36)
(36) 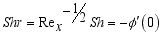 (37)
(37) 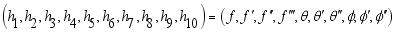 (38)
(38) 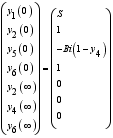 (40)
(40) Ahmad et al. [21] | Hayat et al. [26] | Turkyilmazoglu et al. [27] | Present results | |
|---|---|---|---|---|
0.0 | -1.00000 | -1.00000 | -1.000000 | -1.00000000 |
0.5 | -1.22474 | -1.22474 | -1.224744 | -1.22474487 |
1.0 | -1.41421 | -1.41421 | -1.414213 | -1.41421356 |
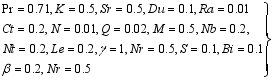 (41)
(41) K | Cf | Nur | Shr |
|---|---|---|---|
0.2 | -2.77175 | 0.06222 | 0.47366 |
0.4 | -2.17873 | 0.06672 | 0.47621 |
0.6 | -1.94287 | 0.06871 | 0.47769 |
Ct | Cf | Nur | Shr |
|---|---|---|---|
0.2 | -2.04041 | 0.06787 | 0.47704 |
0.7 | --2.04040 | 0.06772 | 0.47723 |
0.9 | -2.04039 | 0.06760 | 0.47739 |
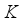 on
on 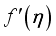 outlined. This developed the momentum boundary layer as a result of
outlined. This developed the momentum boundary layer as a result of 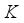 which gives interior heat to the flow and the permeable layer becomes wide. Physically, by enhancing
which gives interior heat to the flow and the permeable layer becomes wide. Physically, by enhancing 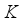 the permeable hole becomes large which leads to the fast flow of fluid. Figure 3 depicts the influence of
the permeable hole becomes large which leads to the fast flow of fluid. Figure 3 depicts the influence of 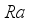 on
on 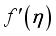 outcome. From the picture, it is clear that the
outcome. From the picture, it is clear that the 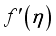 outcome increase with rising values of
outcome increase with rising values of 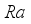 . Actually,
. Actually, 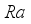 is the proportion of Buoyancy to the product of heat diffusion and viscous. The upshot
is the proportion of Buoyancy to the product of heat diffusion and viscous. The upshot 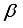 on
on 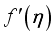 outline is exemplified by Figure 4. By boosting the values of
outline is exemplified by Figure 4. By boosting the values of 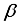 consequently reduced the results of
consequently reduced the results of 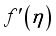 profile.
profile. 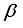 is used to check the fluid material and characters. Although,
is used to check the fluid material and characters. Although, 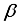 is quite inconsequential if the fluid material materializes. Figure 5 explains the upshot of
is quite inconsequential if the fluid material materializes. Figure 5 explains the upshot of 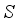 on
on 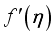 profile with growing values of
profile with growing values of 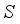 which in turn diminishes the
which in turn diminishes the 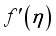 profile. The retarding impact of
profile. The retarding impact of 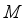 on
on 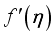 outline is indicated in Figure 6. This physically shows that as
outline is indicated in Figure 6. This physically shows that as 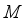 raises it magnifies the magnetic strength and it additionally upsurge the fluid particles which in turn diminishes the
raises it magnifies the magnetic strength and it additionally upsurge the fluid particles which in turn diminishes the 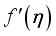 .
. Sr | Cf | Nur | Shr |
|---|---|---|---|
0.2 | -2.04041 | 0.06766 | 0.48656 |
0.6 | -2.04040 | 0.06794 | 0.47387 |
0.8 | -2.04040 | 0.06808 | 0.46754 |
Du | Cf | Nur | Shr |
|---|---|---|---|
0.3 | -2.03952 | 0.05364 | 0.47274 |
0.6 | -2.03823 | 0.03288 | 0.46652 |
0.9 | -2.03700 | 0.01278 | 0.46067 |
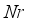 on
on 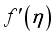 outline. Consequently,
outline. Consequently, 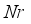 upsurge the buoyance force which improves the fluid velocity. Figure 8 brings foreword the action of
upsurge the buoyance force which improves the fluid velocity. Figure 8 brings foreword the action of 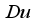 on
on 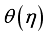 profile. Obviously the raising of
profile. Obviously the raising of 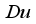 improves the
improves the 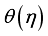 outline. The improvement
outline. The improvement 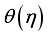 is as results of excessive concentration gradient originate from
is as results of excessive concentration gradient originate from 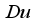 . Also, energy transport and mass diffusion take place in higher rate in the particles which in turn boost the thickness of
. Also, energy transport and mass diffusion take place in higher rate in the particles which in turn boost the thickness of 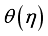 . The features of
. The features of 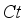 for
for 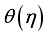 are described in Figure 9 which exhibits raising behavior when
are described in Figure 9 which exhibits raising behavior when 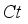 is augmented. This is because
is augmented. This is because 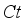 measured the relatively amount of interior energy within the body. Figure 10 Shows
measured the relatively amount of interior energy within the body. Figure 10 Shows 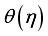 variations for
variations for 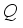 . The upsurge of
. The upsurge of 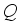 improves
improves 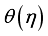 . Basically,
. Basically, 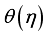 occurrence improved greatly as a result of the presence of
occurrence improved greatly as a result of the presence of 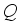 . Figure 11 demonstrates the impact of
. Figure 11 demonstrates the impact of 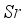 on
on 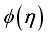 . The upsurge of
. The upsurge of 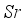 boost
boost 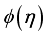 . Thermal gradient has a great effect on
. Thermal gradient has a great effect on 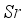 . Actually, greater
. Actually, greater 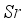 produces greater thermal gradient which in turn upsurged
produces greater thermal gradient which in turn upsurged 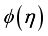 . Figure 12 which exhibits decaling behavior when
. Figure 12 which exhibits decaling behavior when 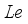 is augmented. Actually,
is augmented. Actually, 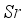 = thermal diffusivity/ mass diffusivity. Figure 13 illustrates the effect of
= thermal diffusivity/ mass diffusivity. Figure 13 illustrates the effect of 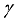 on
on 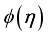 . The upsurge of
. The upsurge of 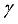 decreases
decreases 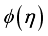 .
. Nb | Cf | Nur | Shr |
|---|---|---|---|
0.5 | -2.04024 | 0.06478 | 0.48772 |
1.0 | -2.03990 | 0.05928 | 0.49139 |
2.0 | -2.03910 | 0.04626 | 0.49336 |
γ | Cf | Nur | Shr |
|---|---|---|---|
1.5 | -2.04041 | 0.06603 | 0.57719 |
2.0 | -2.04042 | 0.06452 | 0.66166 |
4.0 | -2.04039 | 0.05994 | 0.92270 |
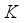 ,
, 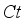 ,
,  ,
, 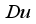 ,
, 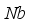 ,
, 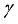 , on
, on 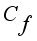 ,
, 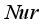 , and
, and 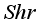 . The outcomes revealed that by considering variations in values of
. The outcomes revealed that by considering variations in values of 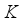 ,
, 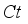 ,
, 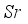 ,
, 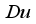 and
and 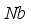 , the magnitude
, the magnitude 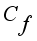 accelerate while it depicts reverse behavior for
accelerate while it depicts reverse behavior for 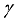 . Also,
. Also, 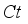 ,
, 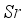 and
and 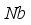 declined the magnitude of
declined the magnitude of 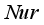 and inclined the magnitude with
and inclined the magnitude with 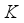 ,
, 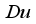 ,
, 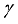 . Similarly, it is experimentally perceived that rise in
. Similarly, it is experimentally perceived that rise in 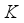 ,
, 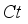 ,
, 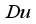 ,
, 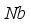 , and
, and 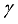 upsurge the
upsurge the 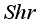 and decelerate with
and decelerate with 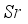 .
. 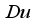 and
and 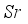 outcome improves
outcome improves 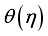 and
and 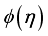 respectively
respectively 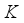 and
and 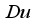 exhibits raising behavior for
exhibits raising behavior for 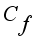 ,
, 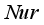 , and
, and 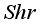
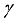 and
and 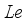 retard the
retard the 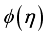 outline
outline 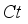 has an escalating effect on the
has an escalating effect on the 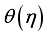 outline
outline Symbol | Description | Symbol | Description | Symbol | Description | Symbol | Description |
|---|---|---|---|---|---|---|---|
Reference temperature | Gravitational acceleration | Prandtl number | Hartmann number | ||||
Dimensionless velocity | Soret parameter | Rayleigh number | Lewis number | ||||
Velocity of the exterior stream | Transverse magnetic field | Buoyancy ratio | Brownian motion parameter | ||||
Condition far away from the plate | Constant | Thermophoresis parameter | Thermal radiation parameter | ||||
Chemical reaction parameter | Electrical conductivity | Magnetic field strength | Density of base fluid | ||||
Kinematic viscosity | Dufour parameter | Velocity components along x, y-axis | T | Temperature variable | |||
Relaxation time | Similarity variable | Nanoparticles specific heat | Ambient liquid concentration | ||||
Stream function | Dimensionless temperature | Heat capacity ratio | Stefan-Boltzmann constant | ||||
Dimensionless concentration | Thermal diffusivity | Nanoparticles concentration | Non-uniform heat generation | ||||
Volumetric thermal expansion coefficient of the base fluid | The fluid viscosity | Mean absorption coefficient | Absorption coefficient | ||||
Fluid specific heat | Deborah number | Ambient liquid temperature | Heat source/sink | ||||
Temperature ratio | S | Mass transfer parameter | Fluid specific heat at constant pressure | Biot number | |||
Thermal conductivity | Brownian diffusion | Termophretic diffusion | Specific heat at constant pressure | ||||
Porous material | Free stream velocity of the flow | Reference concenteration |
| [1] | Ismail, F., Mohamed, B., Mohammed, H. and Abdelkhalek, A. (2020) Analytical and numerical study of Soret and Dufour effects on thermosolutal convection in a Horizontal Brinkman porous layer with a stress free upper Boundary. Mathematical Problems in Engineering. |
| [2] | Safae, H., Abdelkhalek, A., Abdelghani, R., Hassen, B., Mohammed, H., Youssef D. and Haykel, B. (2018) Double- diffusive natural convection in an inclined enclosure with heat generation and Soret effect. Engineering Computation 35: (8) 2753-2774. |
| [3] | Bidemi O. F. and Ahamed M. S. S. (2019). Soret and Dufour effects on unsteady casson magneto-nanofluid flow over an inclined plate embedded in a porous medium. World Journal of Engineerin. |
| [4] | Michael, W. and Isah, B. Y. (2023). On a conducting Jeffrey nanofluid flow over a stretching sheet with porous material and diffusion-thermo: a Lie group approach. Journal of Nanosciences Research & Reports. 5(2): 1-9. |
| [5] | Rana, P., Srikantha, N., Muhammad, T. & Gupta, G., (2021) Computational study of three-dimensional flow and heat transfer of 25 nm Cu–H2O nanoliquid with convective thermal condition and radiative heat flux using modified Buongiorno model. Case Stud. Therm. Eng. 27, 101340. |
| [6] | Madhukesh, J. K., Ramesh, G. K., Prasannakumara, B. C., Shehzad, S. A. & Abbasi, F. M. (2021) Bio-Marangoni convection flow of Casson nanoliquid through a porous medium in the presence of chemically reactive activation energy. Appllied Mathematics and Mechanics. 42(8), 1191–1204. |
| [7] | Puneeth, V., Manjunatha, S., Madhukesh, J. K. & Ramesh, G. K. (2021) Three dimensional mixed convection flow of hybrid casson nanofluid past a nonlinear stretching surface: A modified Buongiorno’s model aspects. Chaos, Solit. Fract. 152, 111428. |
| [8] | Khan, M. I., Qayyum, S., Hayat, T., Khan, M. I., Alsaedi, A.(2019) Entropy optimization in flow of Williamson nanofluid in the presence of chemical reaction and Joule heating, Int. J. Heat Mass Transf. 133: 959–967. |
| [9] | Hayat, T., Khan, S. A., Khan, M. I., Alsaedi, A. (2019) Optimizing the theoretical analysis of entropy generation in flow of second grade nanofluid. Phys. Scr. 94: 085001. |
| [10] | Gireesha, B. J., Sowmya, G., Khan, M. I., ¨Oztop, H. F.,(2019) Flow of hybrid nanofluid across a permeable longitudinal moving fin along with thermal radiation and natural convection. Computer Methods Programs Biomedicine. 185: 105166. |
| [11] | Hussain, F., Subia, G. S., Nazeer, M., Ghafar, M. M., Ali, Z., Hussain, A., (2021) Simultaneous effects of Brownian motion and thermophoretic force on Eyring–Powell fluid through porous geometry. Z. Naturforsch. 5: |
| [12] | Isah, B. Y., Michael, W., Mustafa, A. and Audu, A. (2023). The upshot of nonlinear thermal emission on a conducting Jeffrey nanofluid flow over a stretching sheet: a Lie group approach. Saudi Journal of Civil Engineering, 7(8): 178-191. |
| [13] | Zeid, M. A., Ali, K. K., Shaalanand, M. A., Raslan, K. R. (2019) Numerical study of thermal radiation and mass transfer effects on free convection flow over a moving vertical porous plate using cubic B-spline collocation method. Journal of the Egyptian Mathematics Society |
| [14] | Hayat, T., Saeed, Y., Alsaedi, A., Asad, S. (2015) Effects of convective heat and mass transfer in flow of Powell-Eyring fluid past an exponentially stretching sheet. PLoS ONE 10 (9): e0133831. |
| [15] | Mahanthesh, B., Gireesha, B. J., Gorla, R. S. R., (2016) Heat and mass transfer effects on the mixed convective flow of chemically reacting nanofluid past a moving/ stationary vertical plate. Alex. Eng. J. 55(1): 569–581. |
| [16] | Selimefendigil, F., Coban, S. O., ¨Oztop, H. F., (2021) Numerical analysis of heat and mass transfer of a moving porous moist object in a two dimensional channel. Int. Commun. Heat Mass Transf. 121: 105093. |
| [17] | Ahmed, R., Ali, N., Khan, S. U., Rashad, A. M., Nabwey, H. A., Tlili, I., (2020) Novel micro structural features on heat and mass transfer in peristaltic flow through a curved channel. Front. Phys. 8: 178. |
| [18] | Khan, M., I., Waqas, M., Hayat, T., Alsaedi, A., Muhammad Imran Khan, M., I., (2017), Significance of nonlinear radiation in mixedconvection flow of magneto Walter-B nanoliquid. International Journal of Hydrogen Energy 42: 26408 – 26416. |
| [19] | Ilias, M., R., Aidah Ismail N., S., Raji, N., H., A., Rawi, N., A., and Shafie, S., (2020) Unsteady aligned MHD boundary layer flow and heat transfer of a magnetic nanofluids past an inclined plate. International Journal Mechanical Engineering. 9(2): 197-206. |
| [20] | Jha, B. K. and Samaila G. (2022), Nonlinear approximation for buoyancy-driven mixed convection heat and mass transfer flow over an inclined porous plate with Joule heating, nonlinear thermal radiation, viscous dissipation and thermophoresis effects. Numerical Heat Transfer, Part B: Fundamentals, |
| [21] | Ahmad, B., Nawaz, A., Khan, S. U., Khan, M. I., Abbas, T., Reddy, Y. D., Guedri, K., Malik, M. Y., Goud, B. S., Galal, A. M. (2022), Thermal diffusion of Maxwell nanoparticles with diverse flow features: Lie group simulations. International Communication in Heat and Mass Transfer. 136: 106-164. |
| [22] | Das, K., Sarkary, A. and Kunduz, P. K. (2017), Nanofluid Flow over a Stretching Surface in Presence of Chemical Reaction and Thermal Radiation: An Application of Lie Group Transformation. Journal of Siberian Federal University. Mathematics & Physics. 10(2): 146–157. |
| [23] | Rashidi, M. M. Momoniat, E. Ferdows, M. and Basiriparsa, A. (2014), Lie group solution for free convective flow of a Nanofluid past a chemically reaction horizontal plate in a porous media Hindawi Publishing Corporation. |
| [24] | Kandasamy, R., Loganathanb, P., Arasub, P. P. (2011) Scaling group transformation for MHD boundary-layer flow of a nanofluid past a vertical stretching surface in the presence of suction/injection. Nuclear Engineering and Design 241: 2053-2059. |
| [25] | Li, X. Y., Mishra, S. R., Pattnaik, P. K., Baag, S., Li, M. Y., Khan, I. M., Khan, B. N., Alaoui, K. M., Khan, U. S. (2022) Numerical treatment of time dependent magnetohydrodynamic nanofluid flow of mass and heat transport subject to chemical reaction and heat source, Alexendrial Engineering Journal. 61: (3) 2484–2491. |
| [26] | Hayat, T., Mustafa, M., Pop, I. (2010), Heat and mass transfer for Soret and Dufours effect on mixed convection boundary layer flow over a stretching vertical surface in a porous medium filled with a viscoelastic fluid. Communication Nonlinear Science Numerical Simulation 15: 1183-1196. |
| [27] | Turkyilmazoglu, M. (2013), The analytical solution of mixed convection heat transfer and fluid flow of a MHD viscoelastic fluid over a permeable stretching surface. International Journal mechical science. 77: 263-268. |
APA Style
Williams, M., Yabo, I. B. (2024). The Upshots of Dufour and Soret in Stretching Porous Flow of Convective Maxwell Nanofluid with Nonlinear Thermal Emission. International Journal of Theoretical and Applied Mathematics, 10(3), 38-50. https://doi.org/10.11648/j.ijtam.20241003.12
ACS Style
Williams, M.; Yabo, I. B. The Upshots of Dufour and Soret in Stretching Porous Flow of Convective Maxwell Nanofluid with Nonlinear Thermal Emission. Int. J. Theor. Appl. Math. 2024, 10(3), 38-50. doi: 10.11648/j.ijtam.20241003.12
AMA Style
Williams M, Yabo IB. The Upshots of Dufour and Soret in Stretching Porous Flow of Convective Maxwell Nanofluid with Nonlinear Thermal Emission. Int J Theor Appl Math. 2024;10(3):38-50. doi: 10.11648/j.ijtam.20241003.12
@article{10.11648/j.ijtam.20241003.12,
author = {Michael Williams and Isah Bala Yabo},
title = {The Upshots of Dufour and Soret in Stretching Porous Flow of Convective Maxwell Nanofluid with Nonlinear Thermal Emission
},
journal = {International Journal of Theoretical and Applied Mathematics},
volume = {10},
number = {3},
pages = {38-50},
doi = {10.11648/j.ijtam.20241003.12},
url = {https://doi.org/10.11648/j.ijtam.20241003.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijtam.20241003.12},
abstract = {In this paper, the combined upshot of Soret and Dufoue of a convective Maxwell nanofluid on a porous perpendicular surface with nonlinear thermal emission was investigated. In the present work, the impact of permeable stretching sheet, nonlinear thermal emission, heat sour sink, Dufour and Soret effect, chemical reaction, Brownian motion and thermophoresis in a convective Maxwell nanofluid flow is widely discussed. The governing equations derived for the problem are highly nonlinear coupled partial differential equations. The governing equations were transformed into ordinary differential equations using Lie symmetry group alterations. The BVP4C MATLAB solver was employed to solve the ordinary differential equations numerically after validating the convergence of the method with existing results in the literature. The numerical results were established and discussed using tables and graphs. It was found that variations in porosity parameter (K), Dufour (Du) and Soret (Sr) improves velocity, temperature and concentration profiles respectively and the present of nonlinear thermal radiation and heat source emit more heat for the flow. Also, it is exciting to report that both porosity (K) and Dufour (Du) parameters has a strong impact on the flow of skin frictions, Nusselt number and Sherwood number. However, the current results may present applications in the areas of petroleum reservoir, heat exchangers, steel industries, cooling applications, nuclear waste disposal and so on.
},
year = {2024}
}
TY - JOUR T1 - The Upshots of Dufour and Soret in Stretching Porous Flow of Convective Maxwell Nanofluid with Nonlinear Thermal Emission AU - Michael Williams AU - Isah Bala Yabo Y1 - 2024/10/18 PY - 2024 N1 - https://doi.org/10.11648/j.ijtam.20241003.12 DO - 10.11648/j.ijtam.20241003.12 T2 - International Journal of Theoretical and Applied Mathematics JF - International Journal of Theoretical and Applied Mathematics JO - International Journal of Theoretical and Applied Mathematics SP - 38 EP - 50 PB - Science Publishing Group SN - 2575-5080 UR - https://doi.org/10.11648/j.ijtam.20241003.12 AB - In this paper, the combined upshot of Soret and Dufoue of a convective Maxwell nanofluid on a porous perpendicular surface with nonlinear thermal emission was investigated. In the present work, the impact of permeable stretching sheet, nonlinear thermal emission, heat sour sink, Dufour and Soret effect, chemical reaction, Brownian motion and thermophoresis in a convective Maxwell nanofluid flow is widely discussed. The governing equations derived for the problem are highly nonlinear coupled partial differential equations. The governing equations were transformed into ordinary differential equations using Lie symmetry group alterations. The BVP4C MATLAB solver was employed to solve the ordinary differential equations numerically after validating the convergence of the method with existing results in the literature. The numerical results were established and discussed using tables and graphs. It was found that variations in porosity parameter (K), Dufour (Du) and Soret (Sr) improves velocity, temperature and concentration profiles respectively and the present of nonlinear thermal radiation and heat source emit more heat for the flow. Also, it is exciting to report that both porosity (K) and Dufour (Du) parameters has a strong impact on the flow of skin frictions, Nusselt number and Sherwood number. However, the current results may present applications in the areas of petroleum reservoir, heat exchangers, steel industries, cooling applications, nuclear waste disposal and so on. VL - 10 IS - 3 ER -